Forced Response Surface
Consider a mechanical system of the type
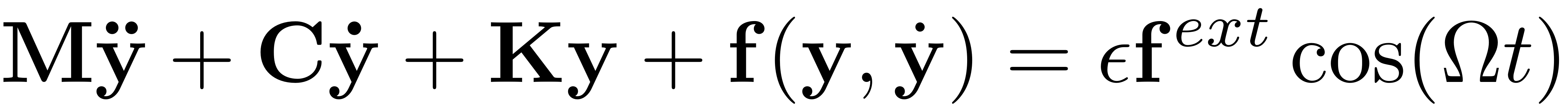
Here,
 is a nonlinear function. We assume that the autonomous system (
is a nonlinear function. We assume that the autonomous system (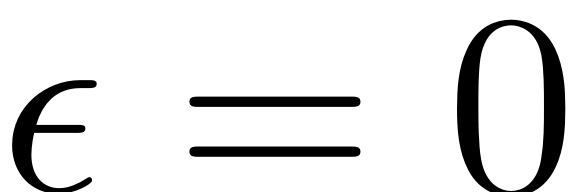 ) admits a hyperbolic fixed point
) admits a hyperbolic fixed point
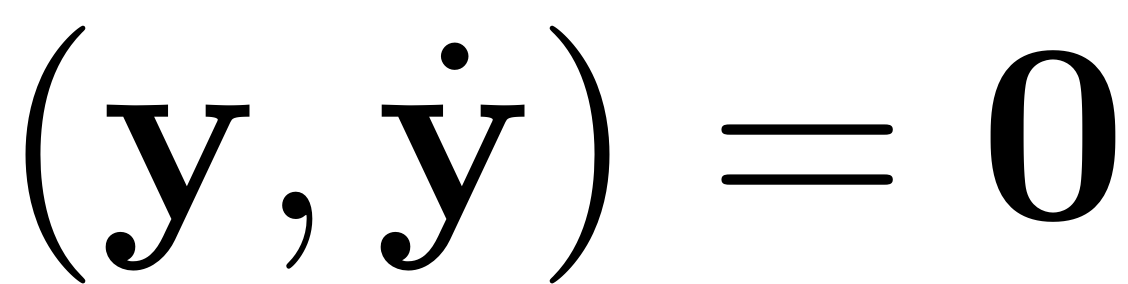 . The under the addition of the harmonic excitation, the fixed point
is perturbed as a periodic orbit of the same stability type. When
. The under the addition of the harmonic excitation, the fixed point
is perturbed as a periodic orbit of the same stability type. When
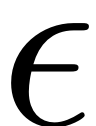 is increased, bifurcations of periodic orbits can be observed. We
have forced response surface (FRS) of periodic orbits under the
variations in forcing frequency
is increased, bifurcations of periodic orbits can be observed. We
have forced response surface (FRS) of periodic orbits under the
variations in forcing frequency
 and forcing amplitude
and forcing amplitude
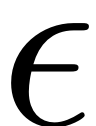 . The FRS is a two-dimensional manifold of periodic orbits. Along
the surface, its ridge is a curve of local maximum under varying
. The FRS is a two-dimensional manifold of periodic orbits. Along
the surface, its ridge is a curve of local maximum under varying
 but fixed
but fixed
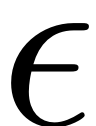 . In other words, a ridge is defined as a family of maximum of FRCs.
Likewise, a trench is defined as a family of minimum of FRCs.
. In other words, a ridge is defined as a family of maximum of FRCs.
Likewise, a trench is defined as a family of minimum of FRCs.
To effeciently extract the FRS, we perform model reduction via spectral submanifolds (SSMs). In particular, a periodic orbit of the original high-dimensinal system is simplified as a fixed point of the SSM-based reduced-order model (ROM). For systems without internal resonances, we can extract the FRS analytically. For systems with internal resonances, one can use two-dimensional parameter continuation of fixed points of the SSM-based ROM to extract the FRS of periodic orbits.
Ridges and trenches characterize the main features of the FRS. Thus, it is instructive to extract the ridges and trenches without computing the surface. This gives a more efficient charaterization of the FRS. We note that ridges and trenches are stationary periodic orbits along forced response curves with fixed forcing amplitudes. This suggests that one can define proper optimization problem to extract the ridges and trenches. Indeed, one can use successive continuation of first-order necessary conditions to extract ridges and trenches.
Detailed treatment of the theory and algorithm extracting FRS and ridges and trenches can also be accessed in the related publication (Li, Jain & Haller, 2024).
Contents
Computation of FRS
After setting up the dynamical system, and the SSM object
S, the FRS can be extracted by using the following
built-in method:
S.extract_FRS(oid,modes,order,mFreqs,parRange,outdof,optdof,scale_state,scale_obs,varargin)
The input arguments are as follows
- oid: runid of continuation
- modes: master subspace
- order: expansion order of SSM
- mFreqs: internal resonance relation vector
- parRange: continuation domain of parameters {[freq1,freq2],[eps1,eps2]}, the frequency range should be near the value of natural frequency with index 1 in the mFreq
- outdof: output for dof in physical domain
- optdof: amplitude at system level (outdof should be a subset of optdof)
- varargin: [{p0,z0}], ['saveICs'] where {p0,z0} are initial solution guesses and saveICs is a flag saving a point on trajectory as initial condition for numerical integration
We note that we can set the method in FRSOptions to be 'level set' or 'continuation'. With 'level set', we extract the FRS analytically. With 'continuation', a two-dimensional continuation algorithm is used to extract the FRS.
Computation of ridges and trenches
After setting up the dynamical system, and the SSM object
S, the FRS can be extracted by using the following
built-in method:
S.extract_ridges_trenches(oid,resonant_modes,order,mFreqs,parRange,outdof,optdof,varargin)
This function extract the damped backbone curve (defined as amplitude resonance) of reduced-order model (in slow phase) as optimization problem of fixed points. Note that this backbone curve will be slightly deviated from the one for a given physical coordinate because the contribution of non-autnomous SSM to the response in physical coordinates. Each equilibirum point corresponds to a periodic orbit in full system. The continuation here starts from the guess of initial solution (for fixed point, adjoints are initialization-free).
The input arguments are as follows
- oid: runid of continuation
- resonant_modes: master subspace
- order: expansion order of SSM
- mFreqs: internal resonance relation vector
- optobj: [] or a structure with fields {optfunc, doptfunc, name}, where optfunc is the optimization objective function doptfunc is the Jacobian of objective function, and name: a string for the fuction name that used in plotting
- parRange: continuation domain of parameters {[freq1,freq2],[eps1,eps2]}, the frequency range should be near the value of natural frequency with index 1 in the mFreq
- outdof: output for dof in physical domain
- varargin: [{p0,z0}], ['saveICs'] where {p0,z0} are initial solution guesses and saveICs is a flag saving a point on trajectory as initial condition for numerical integration
Examples
- FRS of a van Karman Plate.
- Ridges and Trenches of a van Karman Plate.
- FRS of a cantilever beam.
- FRS of a van Karman Shell.
- Ridges and Trenches of a van Karman Shell using the L2 norm.
- Ridges and Trenches of a van Karman Shell using the infinity norm.
